#include <cuda.h>#include <cuda_runtime.h>#include <string>#include <complex>#include <cuComplex.h>#include <stdio.h>#include <enum_quda.h>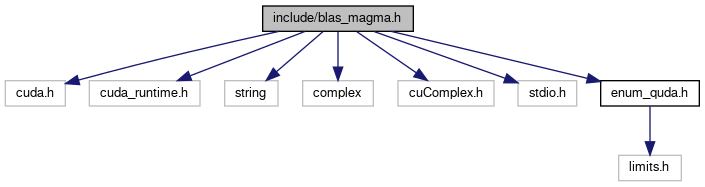
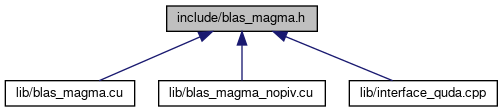
Go to the source code of this file.
Functions | |
| void | OpenMagma () |
| void | CloseMagma () |
| void | magma_Xgesv (void *sol, const int ldn, const int n, void *Mat, const int ldm, const int prec) |
| void | magma_Xgeev (void *Mat, const int n, const int ldm, void *vr, void *evalues, const int ldv, const int prec) |
| void | magma_Xgels (void *Mat, void *c, int rows, int cols, int ldm, const int prec) |
| void | magma_Xheev (void *Mat, const int n, const int ldm, void *evalues, const int prec) |
Function Documentation
◆ CloseMagma()
| void CloseMagma | ( | ) |
Definition at line 323 of file blas_magma.cu.
References errorQuda.
Referenced by closeMagma().

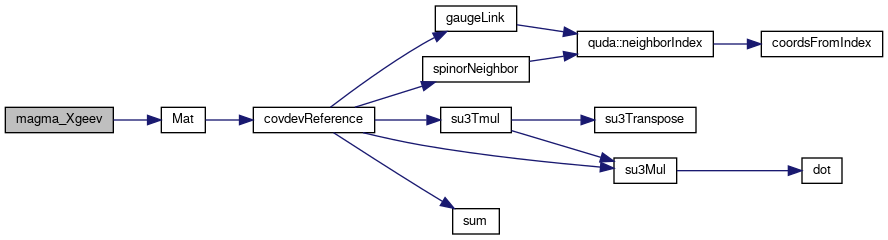
◆ magma_Xgeev()
| void magma_Xgeev | ( | void * | Mat, |
| const int | n, | ||
| const int | ldm, | ||
| void * | vr, | ||
| void * | evalues, | ||
| const int | ldv, | ||
| const int | prec | ||
| ) |
Computes for an n-by-n complex nonsymmetric matrix Mat, the eigenvalues and right eigenvectors.
- Parameters
-
Mat Matrix field containing the input matrices on the CPU n Dimension of the problem ldm Matrix leading dimension vr (out) array containing right eigenvectors evalues (out) array containing eigenvalues ldv Array leading dimension prec Matrix precision
Definition at line 275 of file blas_magma.cu.
References errorQuda, and Mat().
Referenced by quda::ComputeHarmonicRitz< libtype::magma_lib >().

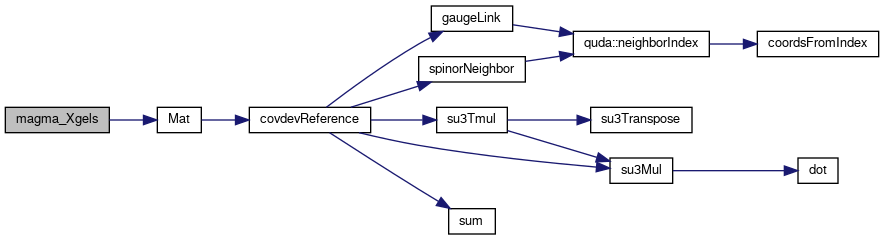
◆ magma_Xgels()
| void magma_Xgels | ( | void * | Mat, |
| void * | c, | ||
| int | rows, | ||
| int | cols, | ||
| int | ldm, | ||
| const int | prec | ||
| ) |
Solves the overdetermined (rows > = cols), least squares problem
- Parameters
-
Mat Matrix field containing the input matrices on the CPU c Array containing source/solution vector rows Number of rows of the matrix Mat cols Number of columns of the matrix Mat ldm Matrix leading dimension prec Matrix precision
Definition at line 286 of file blas_magma.cu.
References errorQuda, and Mat().
Referenced by quda::ComputeEta< libtype::magma_lib >().

◆ magma_Xgesv()
| void magma_Xgesv | ( | void * | sol, |
| const int | ldn, | ||
| const int | n, | ||
| void * | Mat, | ||
| const int | ldm, | ||
| const int | prec | ||
| ) |
Solves a system of linear equations
- Parameters
-
sol (in/out) array containing source (in). Overwritten by solution (out) ldn Array leading dimension n Dimension of the problem Mat Matrix field containing the input matrices on the CPU ldm Matrix leading dimension prec Matrix precision
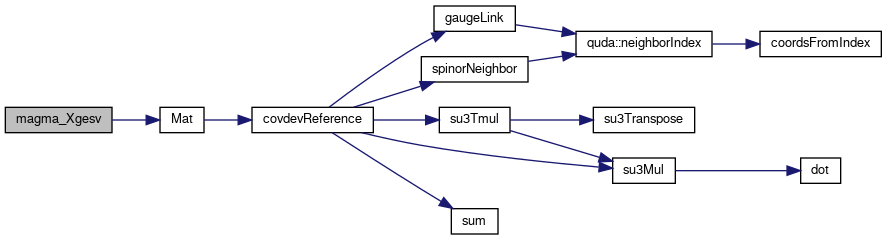
Definition at line 265 of file blas_magma.cu.
References errorQuda, and Mat().
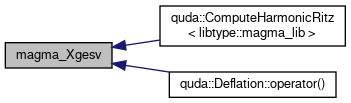
Referenced by quda::ComputeHarmonicRitz< libtype::magma_lib >(), and quda::Deflation::operator()().
◆ magma_Xheev()
| void magma_Xheev | ( | void * | Mat, |
| const int | n, | ||
| const int | ldm, | ||
| void * | evalues, | ||
| const int | prec | ||
| ) |
Computes for an n-by-n complex symmetric matrix Mat, the eigenvalues and eigenvectors.
- Parameters
-
Mat Matrix field containing the input matrices on the CPU, and eigenvectors on exit n Dimension of the problem ldm Matrix leading dimension evalues (out) array containing eigenvalues ldv Array leading dimension prec Matrix precision
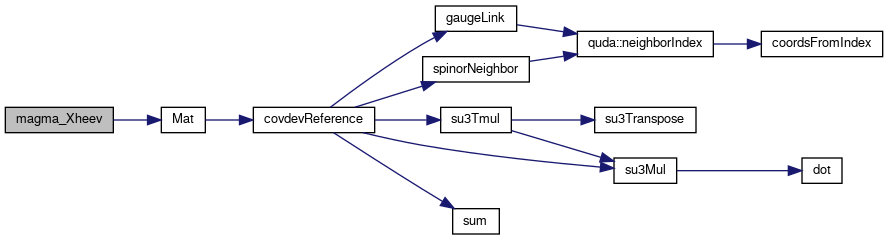
Definition at line 296 of file blas_magma.cu.
References errorQuda, and Mat().
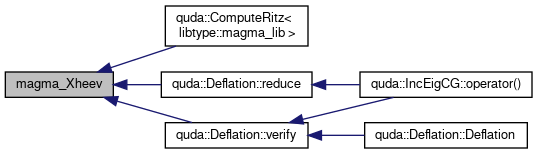
Referenced by quda::ComputeRitz< libtype::magma_lib >(), quda::Deflation::reduce(), and quda::Deflation::verify().
◆ OpenMagma()
| void OpenMagma | ( | ) |
Definition at line 307 of file blas_magma.cu.
References errorQuda, getVerbosity(), printfQuda, and QUDA_VERBOSE.
Referenced by openMagma().


 1.8.13
1.8.13